Assignment #1: Image Classification, kNN, SVM, Softmax, Neural Network
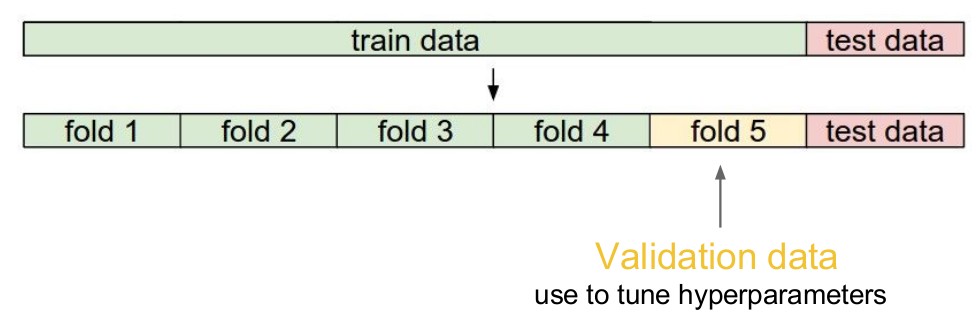
Image Classification: Data-driven Approach, k-Nearest Neighbor, train/val/test splits
$Image\ Classification\ Challenges$
- 视角变化(viewpoint variation)
- 规模变化(Scale variation)
- 形变(deformation)
- 遮挡(occlusion)
- 背景干扰(background clutter)
- 类内差异(intraclass variation)
$Data-driven\ Approach(数据驱动方法)$ 利用数据进行deep learning训练
$ The\ image\ classification\ pipeline(图像分类管道) $
- Input
- Learning
- Evaluation
$ L1\ distance(曼哈顿距离): $
| $d_1 (I_1, I_2) = \sum_{p} \left | I^p_1 - I^p_2 \right | $ |
$L2\ diatance(欧拉距离):$
$d_2 (I_1, I_2) = \sqrt{\sum_{p} \left( I^p_1 - I^p_2 \right)^2} $
$ KNN的不足 $
- 分类器必须记忆所有的训练数据用于预测图片标签。所以当数据量很大时,效率很低。
- 对测试图片分类时需要的计算成本很大,因为要和所有的训练图片进行比对。
Linear classification: Support Vector Machine, Softmax
$dataset\ of\ images\ x_i \in R^D ,\ i = 1 \dots N$
$label\ y_i,\ y_i \in { 1 \dots K } $
$f: R^D \mapsto R^K$
Linear classifier
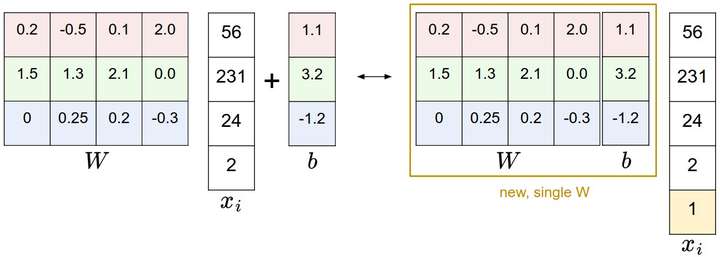
$f(x_i, W, b) = W x_i + b$
** 图像数据预处理: **在实践中,对每个特征减去平均值来中心化数据是非常重要的。在这些图片的例子中,该步骤意味着根据训练集中所有的图像计算出一个平均图像值,然后每个图像都减去这个平均值,这样图像的像素值就大约分布在[-127, 127]之间了。
Multiclass Support Vector Machine Loss fuction
$L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta)$
$y_i 本来的分类,s_j 分类为\ j\ 的score$
$SVM的损失函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值\Delta$
$通常情况下:\Delta = 1.0$
$ s = [13, -7, 11], y_i = 0, L_i = \max(0, -7 - 13 + 10) + \max(0, 11 - 13 + 10)$
$ L_i = \sum_{j\neq y_i} \max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta) $

正则化
$假设有一个数据集和一个权重集W能够正确地分类每个数据(即所有的边界都满足,对于所有的i$ $都有L_i=0)。问题在于这个W并不唯一:$ $可能有很多相似的W都能正确地分类所有的数据。$
** L2损失 **
$ R(W) = \sum_k\sum_l W_{k,l}^2 $
$ L = \underbrace{ \frac{1}{N} \sum_i L_i }\text{data loss} + \underbrace{ \lambda R(W) }\text{regularization loss} \\ $
$ L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)j - f(x_i; W){y_i} + \Delta) \right] + \lambda \sum_k\sum_l W_{k,l}^2 $
$ N是训练集的数据量 $
$L2惩罚倾向于更小更分散的权重向量,这就会鼓励分类器最终将所有维度上的特征都用起来,$ $而不是强烈依赖其中少数几个维度。$

softmax分类器
$ f(x_i; W) = W x_i $

$ L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) \hspace{0.5in} \text {or equivalently} \hspace{0.5in} L_i = -f_{y_i} + \log\sum_j e^{f_j} $

实操事项:数值稳定。编程实现softmax函数计算的时候,中间项$ e^{f_{y_i}}和\sum_j e^{f_j}$因为存在指数函数,所以数值可能非常大。除以大数值可能导致数值计算的不稳定,所以学会使用归一化技巧非常重要。如果在分式的分子和分母都乘以一个常数C,并把它变换到求和之中,就能得到一个从数学上等价的公式:
$ \frac{e^{f_{y_i}}}{\sum_j e^{f_j}} = \frac{Ce^{f_{y_i}}}{C\sum_j e^{f_j}} = \frac{e^{f_{y_i} + \log C}}{\sum_j e^{f_j + \log C}} $
$ set \log C = -\max_j f_j $
f = np.array([123, 456, 789]) # example with 3 classes and each having large scores
p = np.exp(f) / np.sum(np.exp(f)) # Bad: Numeric problem, potential blowup
# instead: first shift the values of f so that the highest number is 0:
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # safe to do, gives the correct answer
** softmax分类器对于分数是永远不会满意的:正确分类总能得到更高的可能性,错误分类总能得到更低的可能性,损失值总是能够更小。但是,SVM只要边界值被满足了就满意了,不会超过限制去细微地操作具体分数。 **
Optimization: Stochastic Gradient Descent(随机梯度下降)
$ 最优化Optimization:寻找能使得损失函数值最小化的参数 W $
不可导的损失函数:由于max操作,损失函数中存在一些不可导点(kinks),这些点使得损失函数不可微,因为在这些不可导点,梯度是没有定义的。但是次梯度(subgradient)依然存在且常常被使用。
- 策略#1:一个差劲的初始方案:随机搜索
bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
loss = L(X_train, Y_train, W) # get the loss over the entire training set
if loss < bestloss: # keep track of the best solution
bestloss = loss
bestW = W
print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)
- 策略#2:随机本地搜索
W = np.random.randn(10, 3073) * 0.001 # 生成随机初始W
bestloss = float("inf")
for i in xrange(1000):
step_size = 0.0001
Wtry = W + np.random.randn(10, 3073) * step_size
loss = L(Xtr_cols, Ytr, Wtry)
if loss < bestloss:
W = Wtry
bestloss = loss
print 'iter %d loss is %f' % (i, bestloss)
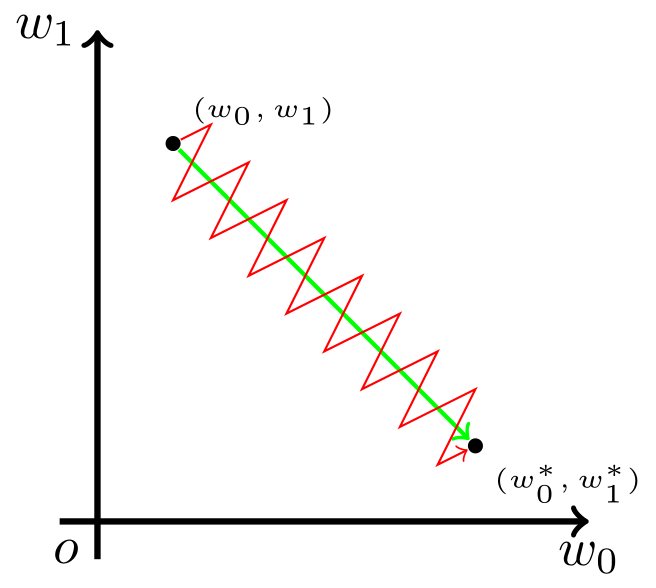
- 策略#3:Follow the slope(跟随梯度)
前两个策略中,我们是尝试在权重空间中找到一个方向,沿着该方向能降低损失函数的损失值。其实不需要随机寻找方向,因为可以直接计算出最好的方向,这就是从数学上计算出最陡峭的方向。这个方向就是损失函数的梯度(gradient)。
在一维函数中,斜率是函数在某一点的瞬时变化率。梯度是函数的斜率的一般化表达,它不是一个值,而是一个向量。在输入空间中,梯度是各个维度的斜率组成的向量(或者称为导数derivatives)。对一维函数的求导公式如下:
$ \frac{df(x)}{dx} = \lim_{h\ \to 0} \frac{f(x + h) - f(x)}{h}$
当函数有多个参数的时候,我们称导数为偏导数。而梯度就是在每个维度上偏导数所形成的向量。

梯度计算
- 使用有限差值进行数值计算
- 微分分析计算梯度
- 利用有限差值计算梯度
#根据上面的梯度公式,代码对所有维度进行迭代,在每个维度上产生一个很小的变化h,
#通过观察函数值变化,计算函数在该维度上的偏导数。最后,所有的梯度存储在变量grad中。
def eval_numerical_gradient(f, x):
"""
一个f在x处的数值梯度法的简单实现
- f是只有一个参数的函数
- x是计算梯度的点
"""
fx = f(x) # 在原点计算函数值
grad = np.zeros(x.shape)
h = 0.00001
# 对x中所有的索引进行迭代
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
# 计算x+h处的函数值
ix = it.multi_index
old_value = x[ix]
x[ix] = old_value + h # 增加h
fxh = f(x) # 计算f(x + h)
x[ix] = old_value # 存到前一个值中 (非常重要)
# 计算偏导数
grad[ix] = (fxh - fx) / h # 坡度
it.iternext() # 到下个维度
return grad
$ 中心差值公式: [f(x+h) - f(x-h)] / 2 h $
效率问题:计算数值梯度的复杂性和参数的量线性相关。在本例中有30730个参数,所以损失函数每走一步就需要计算30731次损失函数的梯度。现代神经网络很容易就有上千万的参数,因此这个问题只会越发严峻。显然这个策略不适合大规模数据,我们需要更好的策略。
微分分析计算梯度
使用有限差值近似计算梯度比较简单,但缺点在于终究只是近似(因为我们对于h值是选取了一个很小的数值,但真正的梯度定义中h趋向0的极限),且耗费计算资源太多。第二个梯度计算方法是利用微分来分析,能得到计算梯度的公式(不是近似),用公式计算梯度速度很快,唯一不好的就是实现的时候容易出错。为了解决这个问题,在实际操作时常常将分析梯度法的结果和数值梯度法的结果作比较,以此来检查其实现的正确性,这个步骤叫做梯度检查。
$ L_i = \sum_{j\neq y_i} \left[ \max(0, w_j^Tx_i - w_{y_i}^Tx_i + \Delta) \right]$
$ \nabla_{w_{y_i}} L_i = - \left( \sum_{j\neq y_i} \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) \right) x_i$
$ \nabla_{w_j} L_i = \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) x_i$
小批量数据梯度下降(Mini-batch gradient descent):在大规模的应用中(比如ILSVRC挑战赛),训练数据可以达到百万级量级。如果像这样计算整个训练集,来获得仅仅一个参数的更新就太浪费了。一个常用的方法是计算训练集中的小批量(batches)数据。
小批量数据策略有个极端情况,那就是每个批量中只有1个数据样本,这种策略被称为随机梯度下降(Stochastic Gradient Descent 简称SGD),有时候也被称为在线梯度下降。这种策略在实际情况中相对少见,因为向量化操作的代码一次计算100个数据 比100次计算1个数据要高效很多。
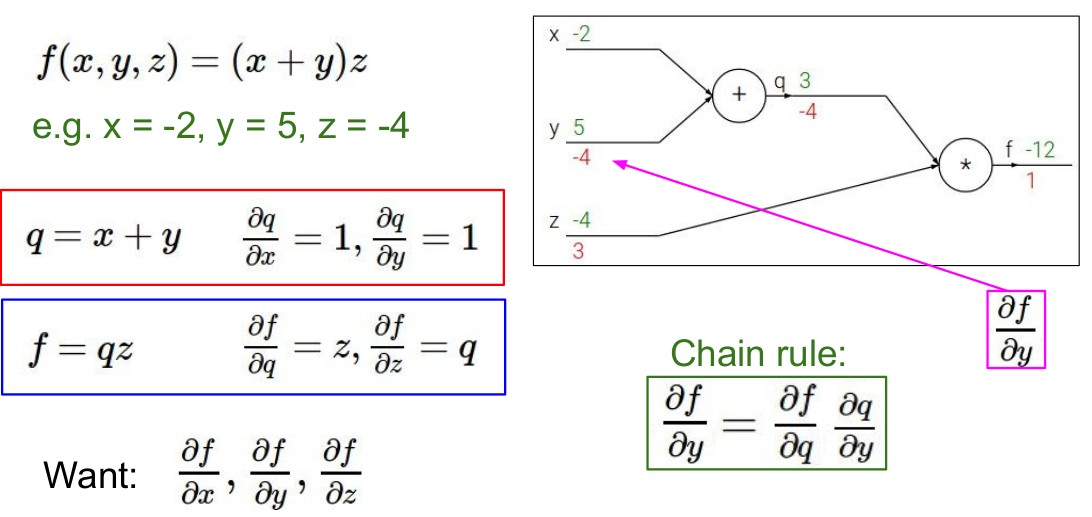
Backpropagation, Intuitions
** sigmod函数**
$ \sigma(x) = \frac{1}{1+e^{-x}} \
\rightarrow \hspace{0.3in} \frac{d\sigma(x)}{dx} = \frac{e^{-x}}{(1+e^{-x})^2} = \left( \frac{1 + e^{-x} - 1}{1 + e^{-x}} \right) \left( \frac{1}{1+e^{-x}} \right)
= \left( 1 - \sigma(x) \right) \sigma(x) $
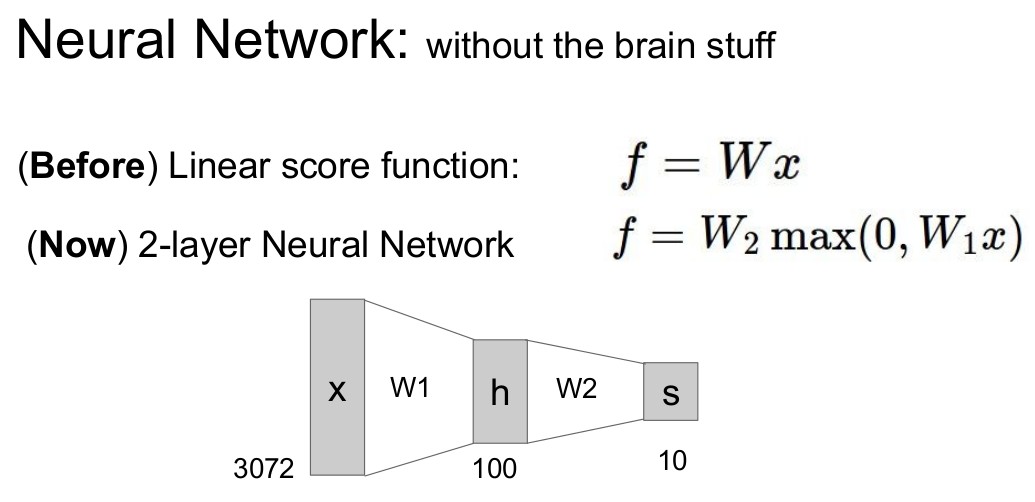
Neural Networks Part 1: Setting up the Architecture
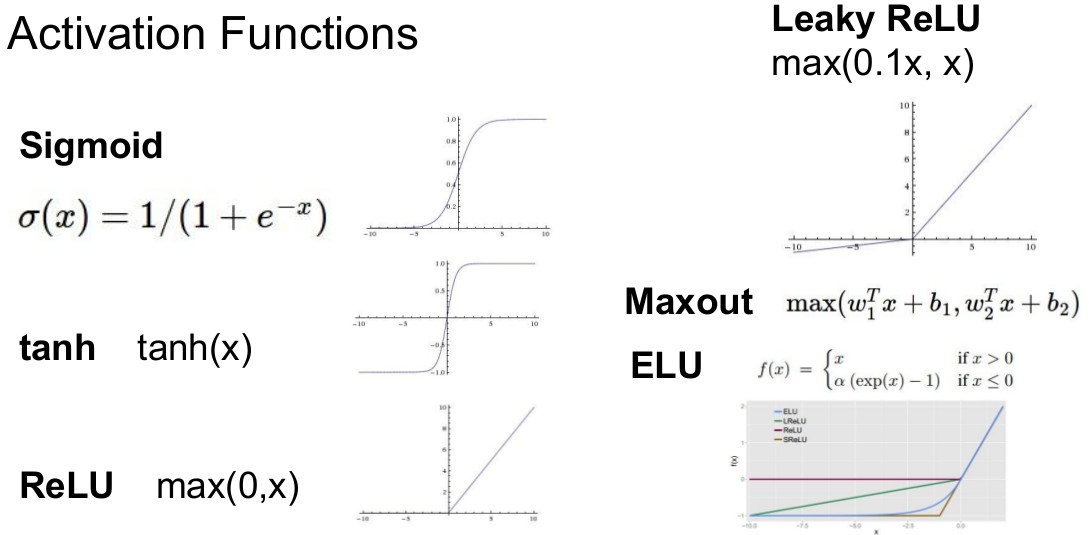
 sigmoid 的两个主要缺点:
sigmoid 的两个主要缺点:
-
Sigmoid函数饱和使梯度消失。sigmoid神经元有一个不好的特性,就是当神经元的激活在接近0或1处时会饱和:在这些区域,梯度几乎为0。回忆一下,在反向传播的时候,这个(局部)梯度将会与整个损失函数关于该门单元输出的梯度相乘。因此,如果局部梯度非常小,那么相乘的结果也会接近零,这会有效地“杀死”梯度,几乎就有没有信号通过神经元传到权重再到数据了。还有,为了防止饱和,必须对于权重矩阵初始化特别留意。比如,如果初始化权重过大,那么大多数神经元将会饱和,导致网络就几乎不学习了。
-
Sigmoid函数的输出不是零中心的。这个性质并不是我们想要的,因为在神经网络后面层中的神经元得到的数据将不是零中心的。这一情况将影响梯度下降的运作,因为如果输入神经元的数据总是正数(比如在f=w^Tx+b中每个元素都x>0),那么关于w的梯度在反向传播的过程中,将会要么全部是正数,要么全部是负数(具体依整个表达式f而定)。这将会导致梯度下降权重更新时出现z字型的下降。然而,可以看到整个批量的数据的梯度被加起来后,对于权重的最终更新将会有不同的正负,这样就从一定程度上减轻了这个问题。因此,该问题相对于上面的神经元饱和问题来说只是个小麻烦,没有那么严重。
** RELU **
- 优点:相较于sigmoid和tanh函数,ReLU对于随机梯度下降的收敛有巨大的加速作用( Krizhevsky 等的论文指出有6倍之多)。据称这是由它的线性,非饱和的公式导致的。
- 优点:sigmoid和tanh神经元含有指数运算等耗费计算资源的操作,而ReLU可以简单地通过对一个矩阵进行阈值计算得到。
- 缺点:在训练的时候,ReLU单元比较脆弱并且可能“死掉”。举例来说,当一个很大的梯度流过ReLU的神经元的时候,可能会导致梯度更新到一种特别的状态,在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生,那么从此所以流过这个神经元的梯度将都变成0。也就是说,这个ReLU单元在训练中将不可逆转的死亡,因为这导致了数据多样化的丢失。(变为负数)例如,如果学习率设置得太高,可能会发现网络中40%的神经元都会死掉(在整个训练集中这些神经元都不会被激活)。通过合理设置学习率,这种情况的发生概率会降低。


$ 现代卷积神经网络能包含约1亿个参数,可由10-20层构成(这就是深度学习)。然而,有效$ $(effective)连接的个数因为参数共享的缘故大大增多。 $
全连接层的前向传播一般就是先进行一个矩阵乘法,然后加上偏置并运用激活函数。
不要减少网络神经元数目的主要原因在于小网络更难使用梯度下降等局部方法来进行训练:虽然小型网络的损失函数的局部极小值更少,也比较容易收敛到这些局部极小值,但是这些最小值一般都很差,损失值很高。相反,大网络拥有更多的局部极小值,但就实际损失值来看,这些局部极小值表现更好,损失更小。
Neural Networks Part 2: Setting up the Data and the Loss
There are three common forms of data preprocessing a data matrix $X$, where we will assume that $X$ is of size $[N x D]$ ($N$ is the number of data, $D$ is their dimensionality).
** 数据预处理 **
均值减法(Mean subtraction)是预处理最常用的形式。它对数据中每个独立特征减去平均值,从几何上可以理解为在每个维度上都将数据云的中心都迁移到原点。在numpy中,该操作可以通过代码$X -= np.mean(X, axis=0)$实现。而对于图像,更常用的是对所有像素都减去一个值,可以用$X -= np.mean(X)$实现,也可以在3个颜色通道上分别操作。
归一化(Normalization)是指将数据的所有维度都归一化,使其数值范围都近似相等。有两种常用方法可以实现归一化。第一种是先对数据做零中心化(zero-centered)处理,然后每个维度都除以其标准差,实现代码为X /= np.std(X, axis=0)。第二种方法是对每个维度都做归一化,使得每个维度的最大和最小值是1和-1。这个预处理操作只有在确信不同的输入特征有不同的数值范围(或计量单位)时才有意义,但要注意预处理操作的重要性几乎等同于学习算法本身。在图像处理中,由于像素的数值范围几乎是一致的(都在0-255之间),所以进行这个额外的预处理步骤并不是很必要。
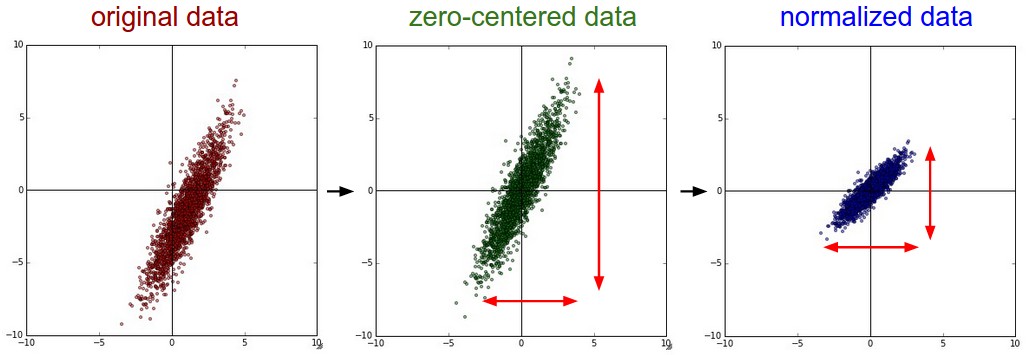
常见错误。进行预处理很重要的一点是:任何预处理策略(比如数据均值)都只能在训练集数据上进行计算,算法训练完毕后再应用到验证集或者测试集上。例如,如果先计算整个数据集图像的平均值然后每张图片都减去平均值,最后将整个数据集分成训练/验证/测试集,那么这个做法是错误的。应该怎么做呢?应该先分成训练/验证/测试集,只是从训练集中求图片平均值,然后各个集(训练/验证/测试集)中的图像再减去这个平均值。