1.论文理解
1.1 数据集的处理
ImageNet包含各种清晰度的图片,而我们的系统要求输入维度恒定,因此,我们对图片进行采样,获得固定大小的256X256的分辨率。对于每张长方形的图,我们将短边按比例调整为256,然后取中心区域的256X256像素。(也有在全连接层加入SPP)
标准化概念 根据数据结构,把数据的值按行,按列,或者某些特征,或者某些属性
- 统一映射到一个特定区间里,比如[-1,1]
- 统一映射到某种特定分布里,比如矩阵为0,方差为1。
Dataset归一化 具体做法就是对于整个训练集图片,每个通道分别减去训练集该通道平均值。
1.2 ReLu
sigmoid 的两个主要缺点:
-
Sigmoid函数饱和使梯度消失。sigmoid神经元有一个不好的特性,就是当神经元的激活在接近0或1处时会饱和:在这些区域,梯度几乎为0。回忆一下,在反向传播的时候,这个(局部)梯度将会与整个损失函数关于该门单元输出的梯度相乘。因此,如果局部梯度非常小,那么相乘的结果也会接近零,这会有效地“杀死”梯度,几乎就有没有信号通过神经元传到权重再到数据了。还有,为了防止饱和,必须对于权重矩阵初始化特别留意。比如,如果初始化权重过大,那么大多数神经元将会饱和,导致网络就几乎不学习了。
-
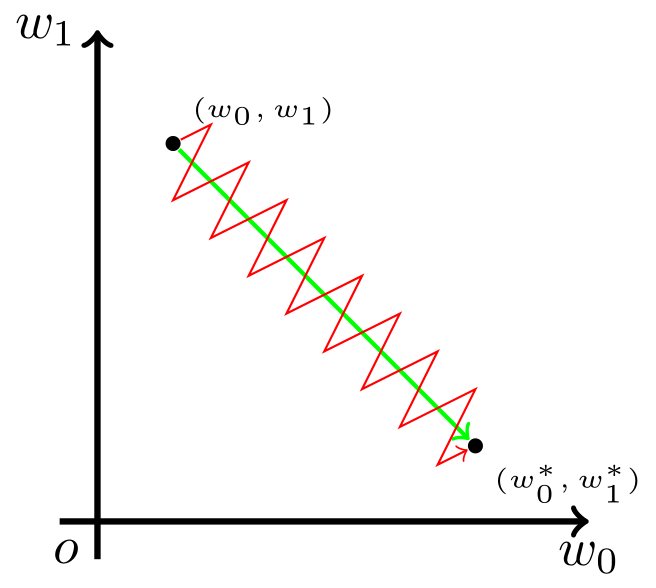
Sigmoid函数的输出不是零中心的。这个性质并不是我们想要的,因为在神经网络后面层中的神经元得到的数据将不是零中心的。这一情况将影响梯度下降的运作,因为如果输入神经元的数据总是正数(比如在f=w^Tx+b中每个元素都x>0),那么关于w的梯度在反向传播的过程中,将会要么全部是正数,要么全部是负数(具体依整个表达式f而定)。这将会导致梯度下降权重更新时出现z字型的下降。然而,可以看到整个批量的数据的梯度被加起来后,对于权重的最终更新将会有不同的正负,这样就从一定程度上减轻了这个问题。因此,该问题相对于上面的神经元饱和问题来说只是个小麻烦,没有那么严重。
RELU
- 优点:相较于sigmoid和tanh函数,ReLU对于随机梯度下降的收敛有巨大的加速作用( Krizhevsky 等的论文指出有6倍之多)。据称这是由它的线性,非饱和的公式导致的。
- 优点:sigmoid和tanh神经元含有指数运算等耗费计算资源的操作,而ReLU可以简单地通过对一个矩阵进行阈值计算得到。
- 缺点:在训练的时候,ReLU单元比较脆弱并且可能“死掉”。举例来说,当一个很大的梯度流过ReLU的神经元的时候,可能会导致梯度更新到一种特别的状态,在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生,那么从此所以流过这个神经元的梯度将都变成0。也就是说,这个ReLU单元在训练中将不可逆转的死亡,因为这导致了数据多样化的丢失。(变为负数)例如,如果学习率设置得太高,可能会发现网络中40%的神经元都会死掉(在整个训练集中这些神经元都不会被激活)。通过合理设置学习率,这种情况的发生概率会降低。
1.3 Training on Multiple GPUs
GTX 580 GPU:内存不够。
因为要存储feature map 和 训练参数。
Gpu之间可以向彼此的存储中做读写操作,不需要通过主机。
采用的并行模式主要是将各一半的网络内核(或神经元)放在每个GPU上,然后再采用一个小技巧:将GPU通信限制在某些特定的层上。
这意味着,比如,第三层的内核从所有的第二层内核映射(kernel map)中获得输入,但是,第四层的内核只从和自己在同一个GPU上的第三层内核中获得输入。采用这种连接模式对于交互验证是个问题,但这允许我们精确调整连接的数量,直到计算量落入一个可接受的范围内。
多个GPU并行可以加速:
The network has 62.3 million parameters, and needs 1.1 billion computation units in a forward pass. We can also see convolution layers, which accounts for 6% of all the parameters, consumes 95% of the computation.
1.4 Local Response Normalization
$b_{x,y}^{i} = a_{x,y}^{i}/(k+\alpha \sum_{j=max(0,i-n/2)}^{min(N-1,i+n/2)}(a_{x,y}^{i})^{2})^{\beta}$
$a[batch,\ height,\ weight,\ channels]$
$N是该层的feature\ map总数,n表示取该feature\ map$
$为中间的左右各n/2个feature\ map来求均值。$
$k,n,\alpha,\beta都是固定值。有些层ReLu之后会有maxPooling$$和LRN$
抑制同一位置其他通道的特征值。
1.5 Overlapping Pooling
通过池化降低conv后的特征,也可以降低过拟合。
max Pooling Overlapping可以让特征大的神经元多次利用,也会让信息丢失更少。如果没有Overlapping,则会导致信息丢失过多,只有少数大的被保留。
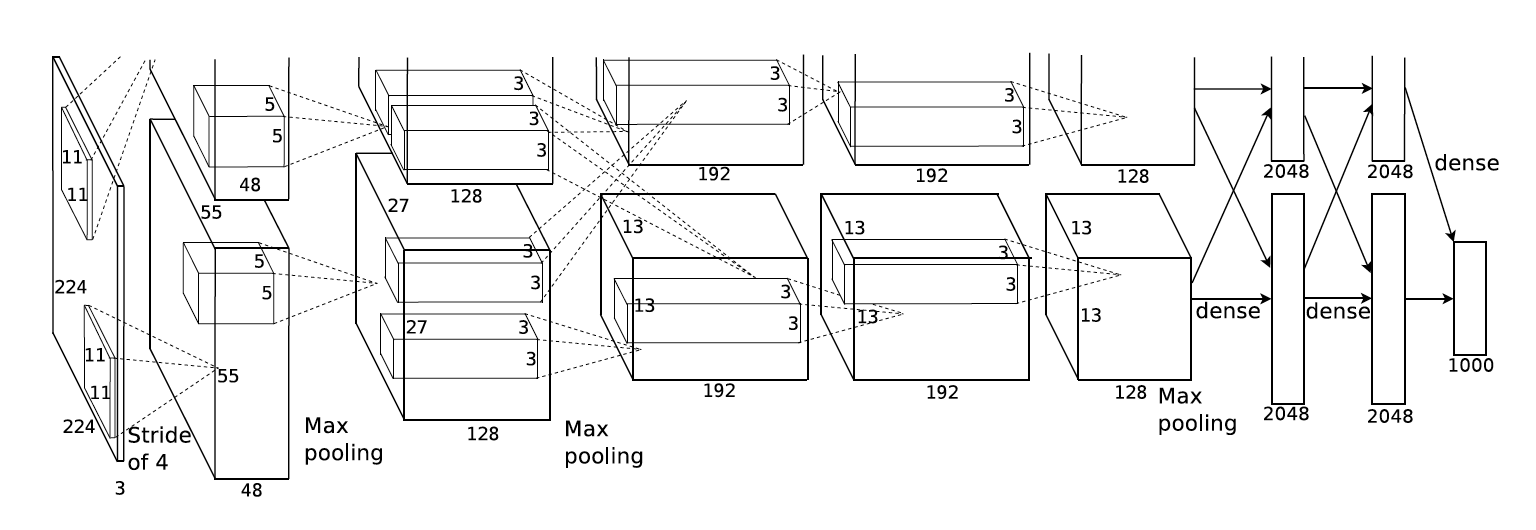
1.6 AlexNet结构
The kernels of the second, fourth, and fifth convolutional layers are connected only to those kernel maps in the previous layer which reside on the same GPU . The kernels of the third convolutional layer are connected to all kernel maps in the second layer. The neurons in the fully- connected layers are connected to all neurons in the previous layer.
Response-normalization layers follow the first and second convolutional layers. Max-pooling layers follow both response-normalization layers as well as the fifth convolutional layer.
1.7 Data Augmentation(数据放大)
最简单最常用的减少过拟合的方法就是利用标签保存变形技术人工放大数据集。我们采取了两种不同形式的数据放大,它们都允许在仅对原图做少量计算的情况下产生变形的新图,所以变形后的新图无需存储在硬盘中。
在我们的实现中,变形的新图由Python在CPU上计算产生,与此同时,GPU仍在计算其他的之前批次的图片。所以这种放大数据集的方式是很高效很节省计算资源的。
第一种是随机裁剪,原图256×256,裁剪大小为224×224,由于随机,所以每个epoch中对同一张图片进行了不同的裁剪,理论上相当于扩大数据集32×32×2=2048倍。在预测(deploy)阶段,不是随机裁剪,而是固定为图片四个边角,外加中心位置。翻转后进行同样操作,共产生10个patch。
第二种数据增强方式包括改变训练图像的RGB通道的强度。具体地,我们在整个ImageNet训练集上对RGB像素值集合执行PCA。对于每幅训练图像,我们加上多倍找到的主成分,大小成正比的对应特征值乘以一个随机变量,随机变量通过均值为0,标准差为0.1的高斯分布得到。因此对于每幅RGB图像像素$I_xy = [I^R_{xy} , I^G_{xy} , I^B_{xy} ]^T$,,我们加上下面的数量:
$[p_1, p_2, p_3][\alpha_1\lambda_1, \alpha_2\lambda_2,\alpha_3\lambda_3]^T$
$p_{i},\lambda_{i}$分别是RGB像素值3 × 3协方差矩阵的第i个特征向量和特征值,$\alpha_{i}$是前面提到的随机变量。对于某个训练图像的所有像素,每个$\alpha_{i}$只获取一次,直到图像进行下一次训练时才重新获取。这个方案近似抓住了自然图像的一个重要特性,即光照的颜色和强度发生变化时,目标身份是不变的。
1.8 Dropout
怎么在训练一个模型的时候,能训练出多个模型,进而使用多个模型来预测,降低测试误差?
dropout是指在深度学习网络的训练过程中,对于神经网络单元,按照一定的概率将其暂时从网络中丢弃。注意是暂时,对于随机梯度下降来说,由于是随机丢弃,故而每一个mini-batch都在训练不同的网络。(也可以降低过拟合)
2.Alexnet实现
2.1 Alexnet结构
- 网络结构
···
class AlexNet(object):
'''
input_x : 输入图片
keep_prob : 全连接层drop out,训练时需要dropout,而在测试时需要将完整的网络因此不需要dropout
num_class : 输出种类,不同的训练集网络差异在于Fc8层的输出神经元,因此我们将类别数设置为参数。
skip_layer : 跳过的层,用于修改Alexnet
weights_path: 权重加载的路径
'''
def __init__(self, input_x, keep_prob, num_classes, skip_layer, weights_path):
self.input_x = input_x
self.keep_prob = keep_prob
self.num_classes = num_classes
self.skip_layer = skip_layer
if weights_path == 'Default':
self.weights_path = 'bvlc_alexnet.npy'
else:
self.weights_path = weights_path
# Create the AlexNet Network Define
self.create()
- 卷积层
由于2012年,GPU性能较弱,内存不够。因此AlexNet通过两个GPU协同训练CNN,在一些层的计算我们需要先将输入以及卷积核分为两组,分别计算然后得到的feature map再合并,因此我们设置了groups参数。
'''
If padding == "SAME":
output_spatial_shape[i] = ceil(input_spatial_shape[i] / strides[i])
If padding == "VALID":
output_spatial_shape[i] = ceil((input_spatial_shape[i] - (spatial_filter_shape[i]-1) * dilation_rate[i]) / strides[i])
'''
def conv(self, input, weightAndHeight, num_kernels, stride, name, padding='SAME', padding_num=0, groups=1):
print('name is {} np.shape(input) {}'.format(name, np.shape(input)))
input_channels = int(np.shape(input)[-1])
'''
pad (tensor ,paddings ,mode = 'CONSTANT' ,name = None ,constant_values = 0)
此操作根据您指定的 paddings 来填充一个 tensor。paddings 是一个具有形状 [n, 2] 的整数张量,其中 n 是 tensor 的秩。
对于每个输入维度 D,paddings [D, 0] 表示在该维度的 tensor 内容之前要添加多少个值,而 paddings[D, 1] 表示在该维度中的 tensor 内容之后要添加多少值。
如果 mode 是 “REFLECT”,那么这两个paddings[D, 0] 和 paddings[D, 1] 不得大于 tensor.dim_size(D) - 1。
如果 mode 是 “SYMMETRIC”,那么这两个 paddings[D, 0] 和 paddings[D, 1] 不得大于tensor.dim_size(D)。
[
[
1, # 第0维,前面补1个(对应tensor的第一维)
2 # 第0维,后面补2个
],
[
3, # 第1维,前面补3个(对应tensor的第二维)
4 # 第2维,后面补4个
]
]
input为四维,第一维是batch,第二维是Height,第三维是Weight,第四维是channel。
'''
if padding_num != 0:
input = tf.pad(input, [[0, 0], [padding_num, padding_num], [padding_num, padding_num], [0, 0]])
'''
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)
input:指需要做卷积的输入图像,它要求是一个Tensor,具有[batch, in_height, in_width, in_channels]这样的shape,要求类型为float32和float64其中之一
filter:相当于CNN中的卷积核,它要求是一个Tensor,具有[filter_height, filter_width, in_channels, out_channels]这样的shape
strides:卷积时在图像每一维的步长,这是一个维度为4的向量
'''
convolve = lambda inputImg, filter: tf.nn.conv2d(inputImg, filter, strides=[1, stride, stride, 1],
padding=padding)
with tf.variable_scope(name) as scope:
weights = tf.get_variable('weights',
shape=[weightAndHeight, weightAndHeight, input_channels / groups, num_kernels])
biases = tf.get_variable('biases', shape=[num_kernels])
if groups == 1:
conv = convolve(input, weights)
else:
'''
tf.split(value, num_or_size_splits,axis=0, num=None,name='split')
axis:第几个维度
'''
input_groups = tf.split(value=input, num_or_size_splits=groups, axis=3)
'''
注意:
input_groups和weights_groups的第三维不同
'''
weights_groups = tf.split(value=weights, num_or_size_splits=groups, axis=3)
output_groups = [convolve(x, y) for x, y in zip(input_groups, weights_groups)]
conv = tf.concat(axis=3, values=output_groups)
withBias = tf.reshape(tf.nn.bias_add(conv, biases), conv.get_shape().as_list())
relu = tf.nn.relu(withBias)
return relu
- maxPooling
def maxPooling(self, input, filter_size, stride, name, padding='SAME'):
print('name is {} np.shape(input) {}'.format(name, np.shape(input)))
'''
tf.nn.max_pool(value, ksize, strides, padding, name=None)
第一个参数value:需要池化的输入,一般池化层接在卷积层后面,所以输入通常是feature map,依然是[batch, height, width, channels]这样的shape
第二个参数ksize:池化窗口的大小,取一个四维向量,一般是[1, height, width, 1],因为我们不想在batch和channels上做池化,所以这两个维度设为了1
第三个参数strides:和卷积类似,窗口在每一个维度上滑动的步长,一般也是[1, stride,stride, 1]
第四个参数padding:和卷积类似,可以取'VALID' 或者'SAME'
返回一个Tensor,类型不变,shape仍然是[batch, height, width, channels]这种形式
'''
return tf.nn.max_pool(input, ksize=[1, filter_size, filter_size, 1], strides=[1, stride, stride, 1],
padding=padding, name=name)
- lrn
def lrn(self, input, radius, alpha, beta, name, bias=1.0):
print('name is {} np.shape(input) {}'.format(name, np.shape(input)))
'''
tf.nn.local_response_normalization(input, depth_radius=None, bias=None, alpha=None, beta=None, name=None)
局部响应归一化原理是仿造生物学上活跃的神经元对相邻神经元的抑制现象(侧抑制):兴奋神经元抑制其邻居的能力
因为ReLU神经元具有无限激活,我们需要LRN来规范化。 我们希望检测具有大响应的高频特征。 如果我们围绕兴奋神经元的局部邻域进行标准化,则与其邻居相比,它变得更加敏感。
同时,它将抑制在任何给定的当地社区中均匀大的响应。 如果所有值都很大,那么对这些值进行标准化会减少所有这些值。
'''
return tf.nn.local_response_normalization(input=input, depth_radius=radius, bias=bias, alpha=alpha, beta=beta,
name=name)
- fc
def fc(self, input, num_input, num_output, name, drop_out=0, relu=True):
print('name is {} np.shape(input) {}'.format(name, np.shape(input)))
with tf.variable_scope(name) as scope:
weights = tf.get_variable('weights', shape=[num_input, num_output], trainable=True)
biases = tf.get_variable('biases', shape=[num_output], trainable=True)
# Linear
act = tf.nn.xw_plus_b(input, weights, biases, name=scope.name)
if relu == True:
relu = tf.nn.relu(act)
if drop_out == 0:
return relu
else:
'''
With probability keep_prob, outputs the input element scaled up by 1 / keep_prob, otherwise outputs 0. The scaling is so that the expected sum is unchanged.' \
The scaling is so that the expected sum is unchanged.
The scaling factor is set to 1 / keep_prob, because the dropout is should be disabled at testing or evaluation.
During testing or evaluation, the activation of each unit is unscaled.
'''
return tf.nn.dropout(relu, 1.0 - drop_out)
else:
if drop_out == 0:
return act
else:
return tf.nn.dropout(act, 1.0 - drop_out)
- 创建网络图
def create(self):
# layer1
conv1 = self.conv(self.input_x, 11, 96, 4, name='conv1', padding='VALID')
pool1 = self.maxPooling(conv1, filter_size=3, stride=2, name='pool1', padding='VALID')
norm1 = self.lrn(pool1, 2, 2e-05, 0.75, name='norm1')
# layer2
conv2 = self.conv(norm1, 5, 256, 1, name='conv2', padding_num=2, padding='VALID', groups=2)
pool2 = self.maxPooling(conv2, 3, 2, name='pool2', padding='VALID')
norm2 = self.lrn(pool2, 2, 2e-05, 0.75, name='norm2')
# layer3
conv3 = self.conv(norm2, 3, 384, 1, name='conv3', padding_num=1, padding='VALID', groups=1)
# layer4
conv4 = self.conv(conv3, 3, 384, 1, name='conv4', padding_num=1, padding='VALID', groups=2)
# layer 5
conv5 = self.conv(conv4, 3, 256, 1, name='conv5', padding_num=1, padding='VALID', groups=2)
pool5 = self.maxPooling(conv5, 3, 2, name='pool5', padding='VALID')
# layer6
flattened = tf.reshape(pool5, [-1, 6 * 6 * 256])
fc6 = self.fc(input=flattened, num_input=6 * 6 * 256, num_output=4096, name='fc6', drop_out=1.0 - self.keep_prob,
relu=True)
# layer 7
fc7 = self.fc(input=fc6, num_input=4096, num_output=4096, name='fc7', drop_out=1.0 - self.keep_prob, relu=True)
# layer 8
self.fc8 = self.fc(input=fc7, num_input=4096, num_output=self.num_classes, name='fc8', drop_out=0, relu=False)
- load_weights
# 通过ImageNet预训练模型初始化我们的各层参数,各层以dict形式存在nparray中,因此我们首先加载模型,然后根据网络的名字分别加载权重及偏置的参数。
# weights_dict['conv1']是一个键为weights和biases字典
def load_weights(self, session):
# 返回可遍历的(键, 值) 元组数组。
weights_dict = np.load(self.weights_path, encoding='bytes').item()
for op_name in weights_dict:
if op_name not in self.skip_layer:
with tf.variable_scope(op_name, reuse=True):
# Loop over list of weights/biases and assign them to their corresponding tf variable
for data in weights_dict[op_name]:
if len(data.shape) == 1:
var = tf.get_variable('biases', trainable=False)
session.run(var.assign(data))
else:
var = tf.get_variable('weights', trainable=False)
session.run(var.assign(data))
- test_image
对于输入图像,我们首先将其大小归一化为网络输入大小,并定义一个占位符用以结果输出,然后加载网络模型,正向传播网络得到FC8层输出结果,然后将softmax结果转换为类别结果。
import cv2
import tensorflow as tf
import numpy as np
from Alexnet import AlexNet
def test_image(path_image, num_class, path_classes, weights_path='Default'):
input = cv2.imread(path_image)
input = cv2.resize(input, (227, 227))
input = input.astype(np.float32)
input = np.reshape(input, [1, 227, 227, 3])
model = AlexNet(input, 0.9, 1000, skip_layer='', weights_path=weights_path)
score = model.fc8
max = tf.argmax(score, 1)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
model.load_weights(sess)
label_id = sess.run(max)[0]
with open(path_classes) as f:
lines = f.readlines()
label = lines[label_id]
print('image name is {} class_id is {} class_name is {}'.format(path_image, label_id, label))
f.close()
test_image('/home/zyc/tensorflow-AlexNet/poodle.png', 1000, 'caffe_classes.py')